MATEMATICAS
El teorema de Pitágoras
Para poder hablar sobre el problema de Pitágoras tenemos que saber quién fue, a continuación un poco de su vida:

Biografía de Pitágoras
(isla de Samos, actual Grecia, h. 572 a.C.-Metaponto, hoy desaparecida, actual Italia, h. 497 a.C.) Filósofo y matemático griego. Se tienen pocas noticias de la biografía de Pitágoras que puedan considerarse fidedignas, ya que su condición de fundador de una secta religiosa propició la temprana aparición de una tradición legendaria en torno a su persona.
Parece seguro que Pitágoras fue hijo de Mnesarco y que la primera parte de su vida la pasó en Samos, la isla que probablemente abandonó unos años antes de la ejecución de su tirano Polícrates, en el 522 a.C. Es posible que viajara entonces a Mileto, para visitar luego Fenicia y Egipto; en este último país, cuna del conocimiento esotérico, se le atribuye haber estudiado los misterios, así como geometría y astronomía.
La voluntad unitaria de la doctrina pitagórica quedaba plasmada en la relación que establecía entre el orden cósmico y el moral; para los pitagóricos, el hombre era también un verdadero microcosmos en el que el alma aparecía como la armonía del cuerpo. En este sentido, entendían que la medicina tenía la función de restablecer la armonía del individuo cuando ésta se viera perturbada, y, siendo la música instrumento por excelencia para la purificación del alma, la consideraban, por lo mismo, como una medicina para el cuerpo. La santidad predicada por Pitágoras implicaba toda una serie de normas higiénicas basadas en tabúes como la prohibición de consumir animales, que parece haber estado directamente relacionada con la creencia en la transmigración de las almas; se dice que el propio Pitágoras declaró ser hijo de Hermes, y que sus discípulos lo consideraban una encarnación de Apolo.
SUS DESCUBIMIENTOS:
En Geometría, su gran descubrimiento fue el teorema que lleva su nombre, y que establece que "el cuadrado de la hipotenusa" de un triángulo rectángulo es igual a "la suma de los cuadrados de los otros dos lados", los catetos.
Los egipcios lo utilizaron de una forma práctica para la construcción de ángulos rectos, hecho de gran utilidad a la hora de realizar obras arquitectónicas. El ángulo opuesto al lado mayor es siempre un ángulo de 90º.
ALGUNAS DEFINICIONES IMPORTANTES:
· ÁREA: Es aquella cantidad de superficie que se encuentra encerrada dentro de una figura geométrica cerrada.
· ÁNGULO: E la abertura entre dos líneas a cualquier tipo que concurre en un punto común llamado vértice
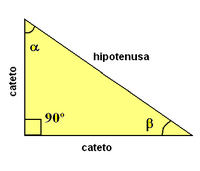
· TRIÁNGULO RECTÁNGULO: es aquel triángulo en el que uno de sus ángulos es recto, es decir mide 90°
¡LA PROBLEMÁTICA EN EL DESCUBRIMIENTO!
Hay cierta controversia acerca de si Pitágoras fue el primero en demostrar el teorema, pues se sabe de la existencia una demostración publicada en la obra matemática Chou Pei, de origen Chino, pudiendo ser ésta anterior a Pitágoras, aunque se cree que no llegó a conocer esta obra.
Actualmente, el Teorema de Pitágoras es de los que cuentan con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración de él para alcanzar el grado de Magíster matheseos (Maestro de las matemáticas).
El matemático estadounidense E. S. Loomis, catalogó 367 pruebas diferentes en su libro de 1927
EL TEOREMA DE PITAGORAS Y SUSU FORMAS DE SACAR:
Este dice que todo triangulo rectángulo, el cuadrado de la hipotenusa (el lado con mayor longitud) es igual a la suma de los cuadrados de los catetos (los otros dos lados del triángulo rectángulo)
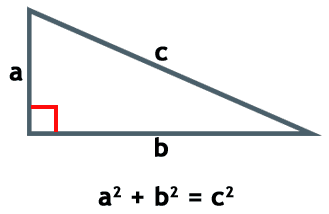
Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²):
a2 + b2 = c2
*también se aplica para el cálculo de un hexágono, en el cual se aplica la siguiente formula:
A= pa/2
P= Perímetro
A= Apotema
TRIGONOMETRIA:
En esta parte del teorema de Pitágoras son utilizadas las razones trigonométricas:
Seno, Coseno, Tangente, Cotangente, Secante y Cosecante (las últimas tres son menos utilizadas comúnmente)
· Seno = cateto opuesto/hipotenusa
· Coseno = cateto adyacente/ hipotenusa
· Tangente = cateto opuesto/ cateto adyacente
· Cotangente = cateto adyacente/cateto opuesto
· Secante = hipotenusa/cateto adyacente
· Cosecante = hipotenusa/cateto opuesto
Estas aparte de ser utilizada para problemas que normalmente vemos en las escuelas también son muy importantes para las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.
HABLEMOS DE ÁNGULOS:
ADYACENTES: Son los ángulos que en un cruce de dos rectas comparten lado:
SUMA DE LOS ÁNGULOS INTERIORES DE UN TRIÁNGULO: Como todos sabemos todos los ángulos interiores de cualquier triangulo al sumarlos dan el resultado de 180°
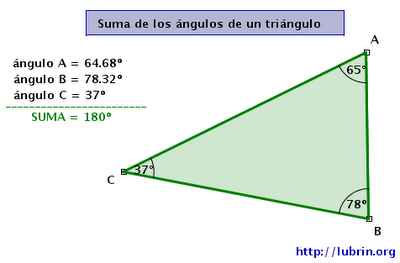
Ángulos opuestos por el vértice:
Los ángulos opuestos por el vértice son congruentes, esto quiere decir:
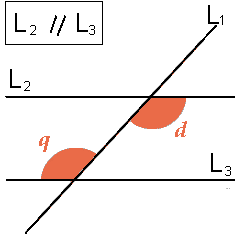
CRIITERIOS DE CONGRUENCIA:
Existen cuatro criterios de congruencia:
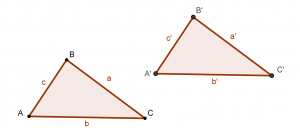
· Criterio primero LLL
Dos triángulos son congruentes si sus tres lado son respectivamente iguales
a = a’
b = b’
c = c’
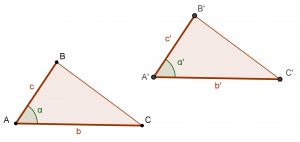
· Criterio segundo LAL
Dos triángulos son congruentes si son respectivamente iguales dos de sus lados y el ángulo comprendido entre ellos:
b = b’
c = c’
α = α’
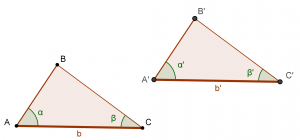
· Criterio tercero ALA
Dos triángulos son congruentes si tienen un lado congruente y los ángulos con vértice en los extremos de dicho lado también congruentes. A estos ángulos se los llama adyacentes al lado.
b = b’
α = α’
β = β’
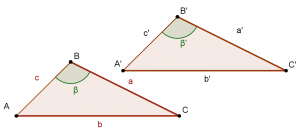
· Criterio cuarto LLA
Dos triángulos son congruentes si tienen dos lados respectivamente congruentes y los ángulos opuestos al mayor de los lados también son congruentes:
a = a’
b = b’
β = β’
Conclusión:
Podemos concluir este tema dando nuestro punto de vista sobre toda esta información publicada, ya que hay veces que nosotros no nos damos cuenta que aunque no parezca estos tipos de problemas se encuentran en cualquier situación de nuestra vida y utilizamos estas sugerencias para solucionar nuestros problemas sin darnos cuenta, ya que todo gira en torno a la matemática, desde una simple resta hasta llegar a grandes ecuaciones, así que nunca está de más saber un poco más sobre el tema y más que nada, hacer que nos parezca interesante, para que sea más fácil de aprender.
¡Por nuestra parte es todo y muchas gracias por leer nuestro blog, comenta que tal te pareció!
EQUIPO:
Miranda Oliva Itzel
Ramírez García Paulo Iván
Haro García Luis Gerardo
Flores del Real Alejandra
Martínez Jiménez Andrea
Rodríguez Gutiérrez Leslie Livier
Vázquez López Alondra Berenice
Rodríguez Corona Josue Joel
